前回の記事まででエントロピー増大則まで導いてきた。

さて、今回の記事では、状態数という考え方やボルツマンの原理などを頼りにさらにエントロピー増大の法則への理解を深めていきたいと思う、って書いていこうと思ったが、あんまりよく分からなかったので、とりあえず今の段階で分かっていることを書いていこうと思う。
1.ボルツマンの原理
エントロピーをS、ボルツマン定数をk、状態数をWとすると以下の式が成り立つ
$$S=klogW$$
いきなり天下り式で申し訳ないが、筆者が導入を書くのが面倒くさいので成り立ちを知りたかったらググってみてほしい。(導入過程は長いが、難しくはないと思う)
ちなみに状態数とは、、、例えば一個のミクロな分子が部屋の中を飛び回っているとする。
それで、その部屋を右側と左側で分けたとき、飛び回っている分子は右側にいるか左側にいるかは確率的に決まる。このとき、一個の分子の状態数は2となる。
ちなみに、N個の分子の系全体のミクロな状態数Wは、
$$W=2^N$$
となる。
ただ、この定義の仕方はすごく曖昧で、Wikipediaなんかを調べてみると、数式である程度厳密な定義がなされている。ただ、まだそこら辺を勉強できていないので、厳密な定義を解説するのはまたいつかということにする。
2.エントロピーと乱雑さ
エントロピーが増大することは乱雑さが増大すると言われる。
この意味について、状態数を手掛かりに考えてみる。
では、ここに10個の分子が空間を自由に飛び回っているとしよう。
そして、ある時に分子が空間の左側か右側かどちらに存在するかを確かめる。ただし、空間を左右で分ける時は、どちらも同じ体積を持つ空間とする。
以下、それぞれの状態における状態数を図式化したものである。
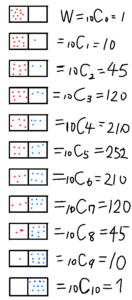
片方に全ての分子が集中している場合が一番状態数が少なく、両方に均等に分布している状態が一番状態数が多い。
自然に考えれば分かる話だが、空気分子を拡散させたときに、すべての分子がある場所に固まっているなんてことはほとんど起こり得ない。
エントロピー増大則から見れば、常にエントロピーは増大し続けるので、ボルツマンの原理より状態数も常に増大すると言える。
したがって、分子は状態数がより多い方向へと進み、それが秩序だった状態からなるべくバラバラに散らばった状態へと変わり続ける。
これがエントロピーが増大することは乱雑さが増大すると言われる所以だ。
(ちなみに、これは曲解かもしれないが、均等に散らばった状況はむしろ秩序だったように見えなくもないのだが。。。まあこの考えは蛇足なのかも)
3.エントロピーと不可逆性
またエントロピーは不可逆性とも関連があると言われる。
再掲だが、状態変化において、エントロピーは減少することなく増加し続ける。
つまり、エントロピーは系自体で減少するということはできないのだ。(ただし、他の系を余分にエントロピーを増大させることで、ある系のエントロピーを減少させる事はできる。だが、系全体で見ればエントロピーは増大している。)
これはつまり、状態変化においては変化を逆にして元に戻ることは不可能であるということだ。
だから、可逆変化は理想的な状況でしか起こり得ず、現実世界では起こらないのだ。どうしても現実世界では不可逆変化になってしまう。
これは、エントロピー増大則が時間の流れる向き(時間の矢)を定めているとも言えるのだ!
4.まとめ
とりあえず、ここで物理学の熱力学連載記事は休止とする。次は一旦力学に戻って、弾性力学という学問を少しまとめてみたいなと思っている。
ただ、熱力学に関してもまだ知識が中途半端なので後でもう一度おさらいをしに戻ってくると思う。
感想だが、とりあえずエントロピーっていう概念が今まではマジで意味不明な概念だったし、熱力学と関係があるということすら分からなかったが、表面だけは数式ベースで掬えたので今のところは満足だ。
特に時間の矢って概念は奥深いなぁーと思った。どうしても哲学好きな身からすると時間とか空間とかの話を聞くとウホウホしたくなる。
それではまた後ほど

コメント