今まで物理の分野では初等力学に関する内容を当ブログで記事にしてきた。ただ筆者は熱力学も最近学び始めたので、それの備忘録として熱力学分野に関する記事をこれから書いていこうと思う。
今回の記事では、熱力学で重要な意味を持つ熱力学第一法則について解説していく。
1.ジュールの実験・熱力学第一法則
1847年にジュールは実験で熱量1kcalが何kgf・mの仕事に相当するかを調べた。
以下は実験の簡単な模式図(図1)。水槽内の水中に羽根車を入れて、その羽根車に糸でおもりを繋げる。そして、つなげたおもりを自由落下させることで羽根車を回し水を撹拌させて、摩擦熱でどれだけ水が温まるかを調べた。
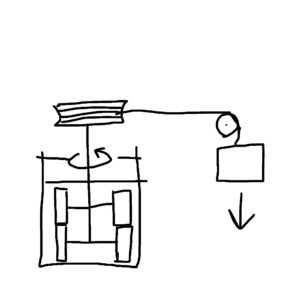
図1 ジュールの実験
結果、1kcal=426.9kgf・mと分かった。
このように、おもりがなした仕事は熱に転化されるという事実が認識されるようになった。そして、仕事はエネルギーの一形態と見ることができることから熱もエネルギーの一形態として認識されるようになる。
つまり、熱も仕事もエネルギーとして相互に変換することができる。という法則にたどり着き、これが熱力学第一法則と呼ばれるようになった。
ところで、エネルギーにおいてはエネルギー保存則が成り立つことから、熱力学第一法則はエネルギー保存則とも呼ばれる。
エネルギー保存則は物理学の最も基本的な法則の一つだ。
↓参考記事

2.熱力学第一法則の式
数式で考えてみる。
物体に加えられた熱量をQ[J]、物体になされた仕事をW[J]、物体の内部エネルギーの変化をΔU[J]、とすると、熱力学第一法則は
$$ΔU=Q+W・・・(1)$$
と表せる。
さらに、シリンダとピストンによって閉じ込められた気体について考えてみる。(図2参照)
気体の圧力はPで、体積がΔVだけ変化したとすると、その時気体になされる仕事Wは
$$W=-PΔV$$
これを(1)式に代入し、両辺を微分すると、
$$dU=dQ-PdV$$
となる。これは熱力学第一法則を微分系で表したものだ。
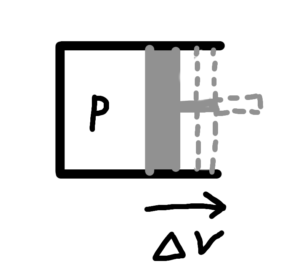
図2 シリンダ内の気体がする仕事
3.熱機関とカルノーサイクル
先ほどのジュールの実験では力学的エネルギーを熱エネルギーへを変換していたが、もちろん熱力学第一法則によって、熱エネルギーを力学的エネルギーにも変換できる。
こうした熱エネルギーを力学的エネルギーに変換する装置を熱機関という。熱を移動させることによって仕事を生み出す装置だ。
以下熱機関の模式図を示す。
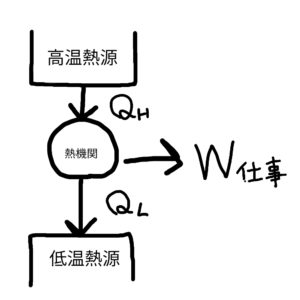
図3 熱機関の模式図
そして、熱機関にカルノーサイクルというものがあるのだが、これについて理解すると熱力学への理解も大分深まるのでこれからカルノーサイクルについて軽く解説していく。
カルノーサイクルは以下のようなPV線図上で、一連のサイクルを繰り返す熱機関である。
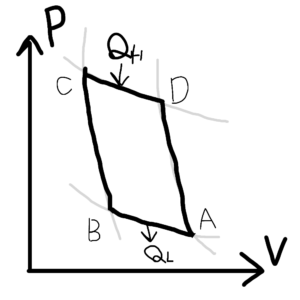
図4 カルノーサイクル
A→B では、等温圧縮。B→C では、断熱圧縮。C→D では、等温膨張。D→A では、断熱膨張を行っている。図4の上部から来ているQHは高温熱源から熱を取り入れていることを意味し、QLは低温熱源へと熱を捨てていることを意味する。
また、ABCDの頂点で構成されるサイクル内の面積が熱機関がなす仕事である。
ところでカルノーサイクルとは、系としてのサイクルの周囲も含めて逆行可能なので可逆変化をする熱機関である。
そして、カルノーサイクルという可逆機関の熱機関は熱効率が最大であることが分かっている。
そもそも熱効率とは何かというと、熱効率をe、図3のようにそれぞれ式を定義すると、
$$e=\frac{W}{Q_{H}}=\frac{Q_{H}-Q_{L}}{Q_{H}}=1-\frac{Q_{L}}{Q_{H}}$$
ちなみになぜカルノーサイクルの熱効率が最大になるかは、詳しくは解説しないが、超カルノーサイクルというカルノーサイクルを上回るカルノーサイクルを考えてみると無からエネルギーを生み出す永久機関ができてしまうことから、結局カルノーサイクルが熱効率最大と証明される。
また、カルノーサイクルの熱効率が最大であることから、「温度の定められた2つの熱源の間にはたらく可逆機関の効率は全て等しく、この効率を超える熱機関は存在しない。」というカルノーの定理が導かれる。そして、これは「可逆機関の効率は2つの熱源の温度だけで決まる」とも捉えることができる。
この考えを考慮すると、以下の式のように可逆機関における熱の比は、温度の比と等しいと表現できる。
$$\frac{Q_{H}}{Q_{L}}=\frac{T_{H}}{T_{L}}$$
ここで、THを可逆機関の高温熱源の温度、TLを可逆機関の低温熱源の温度とおいた。
4.まとめ
今回の熱力学の記事では、可逆機関における熱量の比は温度の比と捉えられるところまで解説した。次回からはこの最後に導いた式からエントロピーの概念を導入して熱力学第二法則に関して解説していく。
次回の記事

<参考文献>
丸茂榮佑 木本恭司 著 「工業熱力学」、コロナ社、二〇〇一年
野田学 著 「理系のための はじめて学ぶ物理[熱力学]」、ナツメ社、二〇〇八年

コメント