「減衰の無い一自由度系の自由振動」をわかりやすく解説

おはこんばんにちは、senehataです。

前回の記事で振動力学の基礎の基礎について解説しました。

今回は振動力学の基礎を踏まえたうえで「減衰のない一自由度系の自由振動」について解説していこうと思います。減衰や固有振動数の知識がある前提で解説するので、それが分からない方は前回の記事を参照することを推奨します。

減衰のない一自由度系の自由振動とは何？

まずは「減衰のない一自由度系の自由振動」という言葉の意味を解説する。ここで言う、減衰とは前記事でも書いたが、速度に応じて比例する抵抗力である。その減衰が無いということは抵抗を考慮しない理想状態で考えるということだ。

自由度についても前記事で書いた。一自由度系とはつまり、並進方向に一方向。もしくは回転の軸が一方向しかない状態を指す。例えていうなら、X軸上でしか動けない物体を考えてみるということだ。

ちなみに、もちろん二自由度系や多自由度系に関する振動の理論は存在するが、一自由度系の理論の方が理解しやすいと思うのでまずは一自由度系の理論に注目していく。

最後に自由振動だが、これは最初に物体が振動する力を加えた後は、外から一切の力を加えない振動のことである。ちなみに、外力を途中で加える振動を強制振動という。

「減衰の無い一自由度系の自由振動」の運動方程式を考えてみる。

まずは、この振動の様子を図１で示す。

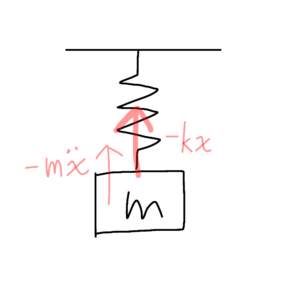
図１　振動の無い一自由度系の自由振動の図

構造としては極めて単純で、質量mの物体にばね定数ｋのばねを付けて、それを天井にぶら下げている。また、慣性力 $-m\ddot{x}$ と復元力 $-kx$ が働いている。

慣性力と復元力以外に働く力は無いので

$$m\ddot{x}+kx=0…(1)$$

変形して、

$$\ddot{x}+\frac{k}{m}x=0…(2)$$

(2)式を減衰の無い一自由度系の自由振動の運動方程式と呼ぶ

また、ここで固有円振動数を式(3)のように定義する。

$$\frac{k}{m}=\omega_{n}^2…(3)$$

よって、(2)式は固有円振動数を用いると、式(4)のように表される

$$\ddot{x}+\omega_{n}^2x=0…(4)$$

また、この運動方程式の解について解くと以下のようになる。(計算過程は割愛)

$$x=\sqrt{x_{0}^2+(\frac{v_{0}}{\omega_{n}})^2}\cos (\omega_{n}t-\tan^{-1} \frac{v_{0}}{x_{0}\omega_{n}})$$

(1)式で重力$mg$が無かったのだが、それについて軽く触れておこう。

それは図１における基準点を、質量mをばねに吊るした状態(既に重力が働いている)における質量mの中心を原点と定めたからである。

つまり(1)式中の$x$は、その中心からどれだけ離れているかを意味する。

ちなみに、(1)式中の$x$を、ばねにおもりを吊るしていない状態で定めた場合には、重力を(1)式中でも考慮する必要がある。

式展開から重力を考慮しなくても良いことを証明もできるが、それについては参考文献(2)に譲る。

今回は「減衰の無い一自由度系の自由振動」について解説した。減衰の無いバージョンだとまだまだ振動力学とまで行かなくても、単純な初等力学の範疇内である気がする。

ただ、次回書く予定の減衰アリバージョンは本格的に振動力学っぽくなってくるので、楽しくなってくると思う。

参考文献

(1)井上順吉・松下修己：機械工学基礎講座　機械力学Ⅰー線形実践振動論、オーム社、2003

(2)藤田聡・古屋治・皆川佳祐：はじめての振動工学、東京電機大学出版局、2019