「減衰のある一自由度系の自由振動」をわかりやすく解説

おはこんばんにちはsenehataです

前回は「減衰のない一自由度系の自由振動」を解説しましたが、今回は「減衰のある一自由度系の自由振動」について解説します。

物体が振動するとなると摩擦や空気抵抗などで徐々に振動は弱まりますが、こういう振動が徐々に弱まることを減衰すると表現します。

前回は減衰しない自由振動でしたが、今回は減衰がある自由振動なのでより現実により近い現象を考察することになります。その分数式は複雑になりますが、考察が深まるので面白いかも。

運動方程式

「減衰のある一自由度系の自由振動」の運動方程式を考えてみる。

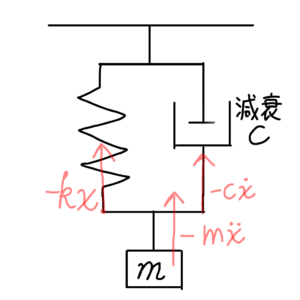
振動の様子を図１に示す

図１　減衰のある自由振動

おもり(質量m)に、慣性力 $-m\ddot{x}$ と復元力 $-kx$ と減衰力$-c\dot{x}$が働いている。

また、基準点を質量mをばねに吊るした状態における質量mの中心に定めた。よって、図１中の$x$は、その中心からどれだけ離れているかを意味する。

慣性力と復元力と減衰力の他に働く力はないため、

$$m\ddot{x}+c\ddot{x}+kx=0…(1)$$

両辺をmで割ると

$$\ddot{x}+\frac{c}{m}\dot{x}+\frac{k}{m}x=0…(2)$$

ここで減衰比$\zeta$を以下のように定義し、また固有円振動数$\omega_{n}$を導入すると

$$\zeta=\frac{c}{2\sqrt{mk}}=\frac{c}{2\sqrt{m^2\frac{k}{m}}}=\frac{c}{2m\omega_{n}}…(3)$$

減衰比については後でまた登場する

(1)式の解を$x=e^{st}$と仮定すると、(1)式は以下のようになる。

$$ms^2+cs+k=0…(4)$$

(4)式はsの二次方程式だから、解の公式より、

$$s=-\frac{c}{2m}\pm j\sqrt{\frac{k}{m}-(\frac{c}{2m})^2}…(5)$$

また、(5)式の根号内は以下のように変形できる

$$\sqrt{\frac{k}{m}-(\frac{c}{2m})^2}$$

$$=\sqrt{\frac{k}{m}}\sqrt{1-\frac{m}{k}•\frac{c^2}{4m^2}}$$

$$=\omega_{n}\sqrt{1-\zeta^2}…(6)$$

よって、(5)(6)式より

$$s=-\frac{c}{2m}\pm j\omega_{n}\sqrt{1-\zeta^2}…(7)$$

(7)式より、sの解は根号内の正負によって変わるように考えられる。

よって、減衰比$\zeta$によって運動方程式の解がどのように変わるかを調べる。この減衰比の大きさによって振動の振る舞いが大きく変わることが示されることになる。

それについては次の記事で書こうと思う。

参考文献

(1)井上順吉・松下修己：機械工学基礎講座　機械力学Ⅰー線形実践振動論、オーム社、2003

(2)藤田聡・古屋治・皆川佳祐：はじめての振動工学、東京電機大学出版局、2019