統計学の重要概念「正規分布」を実際例を踏まえて解説

※※すいません。この記事は中途半端なところで終わってしまってます。情報収集には向いていないので、それでも良い方はお読みくださいませ。※※

前回の記事では、統計の身近な例をなるべく分かりやすく解説しました。

この記事では「生活の中にある身近なものを、統計学によって、なるべく簡単に面白く解説すること」を目的としています。また、統計の知識を持つことは世の中に氾濫するデータを正しく判断し、取捨選択する能力に直結するので、現代社会を上手く生きていくには...

前回は入門的な内容が多かったですが、今回の記事ではいよいよ本格的に統計学の内容に入っていこうと思います。

そこで、今回は「正規分布」という統計学上、大切な概念をなるべく分かりやすく解説しようと思います。高校１年生程度の数学レベルが要求されますが、なるべく分かりやすく解説するので安心してください。

１．正規分布は何に使えるの？

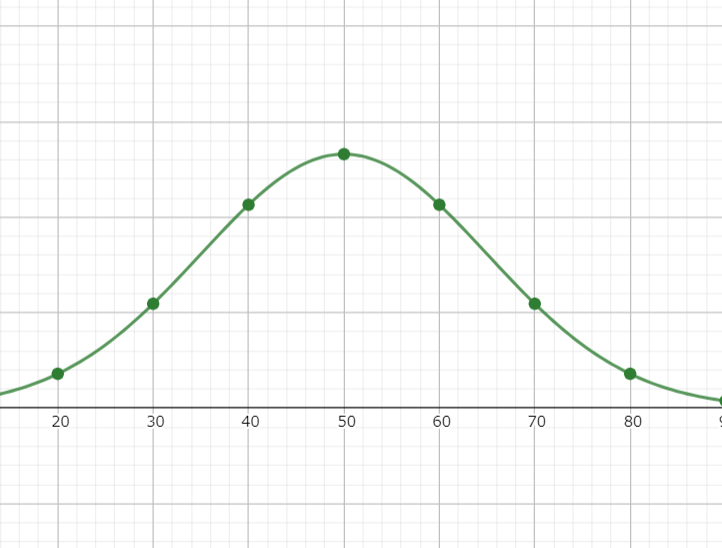
まずは、正規分布のグラフを貼ろうと思います。

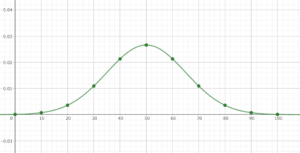
上図のグラフはGeogebraという計算ソフトで描画したものです。上図の様に正規分布は左右対称の山のような形をしています。

このグラフを使って何が分かるかというと例えば、テストの偏差値から自分の全体から見た立ち位置を把握したり、任意の確率でデータがある範囲の値に入ることを予想することができたりします。また、視聴率がどのくらい信頼できる指標なのか、どのくらい誤差があるのかといった判断に役立ちます。

２．正規分布のグラフから分かること

以下が正規分布のグラフの式の値です。

σは標準偏差（分散にルートを取ったもの）、μは平均値です。

exp()とはネイピア数eの指数部分を()の中に入れたものです。例えば、e^xは、exp(x)と同じ値を表します。
（e=2.718281…）

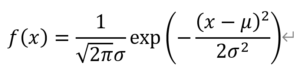
さて、色々書き込みがありますが、正規分布のグラフをもう一度貼ります。

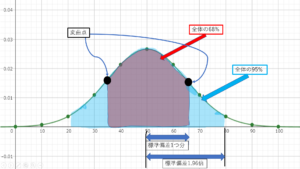
このグラフでは、σ（標準偏差）を15、μ（平均値）を50としました。上図を見ると、下の所に青い矢印がありますが、その矢印の長さは標準偏差の値によって変わります。今回は、標準偏差を15と設定したので、上図のような矢印の長さになってます。

そして、この矢印の長さは何を表しているのかというと、正規分布の赤い部分に注目してください。赤い部分の横幅は平均値（上図の場合は50）から左右に15だけありますが、この15という値は先ほど解説した標準偏差の値と対応します。そして、横幅が正規分布2つ分の赤い部分は何を表すのかというと、全体の約68%のデータが赤い部分に入ることを表します。

例えば、標準偏差15点、平均値50点のテストがあって、テスト受験者の得点分布が正規分布のようなきれいな形になった場合、テスト受験者の約68%が赤い部分に入る。言い換えれば、35点～65点の間に約68%の受験者が含まれることを意味します。

また違う使い方もできて、標準偏差15点、平均値50点のテストで自分が65点を取った場合は、自分が上位16％に入っていることが分かります。

そして、もう一つ上図を見て分かることは水色の部分もあるということで、この水色の部分の横幅の長さは標準偏差1.96倍分で、この長さ分左右に広がっています。そして、この水色の部分に全体の約95%のデータが入ります。具体的な使い方は赤色の部分と全く同じです。

※高校の数学Ⅲを取った人のための補足
上図に変曲点といった場所がありますが、曲線の凹凸が変わる部分を指します。

３．正規分布で偏差値を考えてみる

世間一般の受験生は偏差値というものと関わらざるを得なくて、偏差値を少しでも上げるために必死に勉強します。そして、模試の偏差値が上がったか下がったかで一喜一憂します。

こんな風に受験生を振り回す偏差値ですが、この偏差値は正規分布と密接に関わっています。

まず、偏差値を算出する計算式がこれです。

・・・

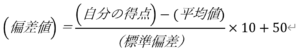
と、この続きを書こうと思っていますが、どうもモチベーションが続かないのでここで一旦区切ります。

続きは後程上げるか更新するかしようと思います。